Generating Equivalent Numerical Expressions Module 9 Page 285 Review
GENERATING EQUIVALENT ALGEBRAIC EXPRESSIONS
An algebraic expression is a mathematical sentence involving constants (any real number), variables and the algebraic operations (add-on, subtraction, multiplication, partition and exponentiation by an exponent that is a rational number).
Let us consider the algebraic expression which is given below.
7(x - three) + 2(2x - five) - 3(x - 5) --------- (1)
To generate equivalent algebraic expression, we accept to simplify.
Let united states of america simplify the expression as given below.
Pace i :
Distributing the number which is exterior the parenthesis with inner terms.
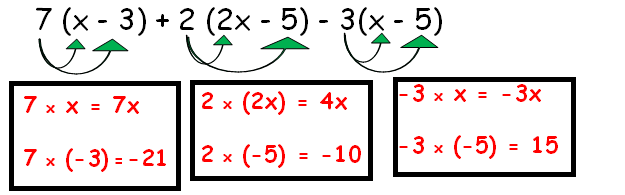
= 7x - 21 + 4x - 10 - 3x + xv
Stride two :
Combine the similar terms
= 7x + 4x - 3x - 21 - 10 + 15
= 11x - 3x - 31 + 15
= 8x - 16
Hence, equivalent algebraic expression to (1) is (8x - sixteen)
Practice Problems
Trouble 1 :
Write the equivalent algebraic expression for the function defined by
f(10) = (xtwo - 5x + 6) / (x - iii)
Solution :
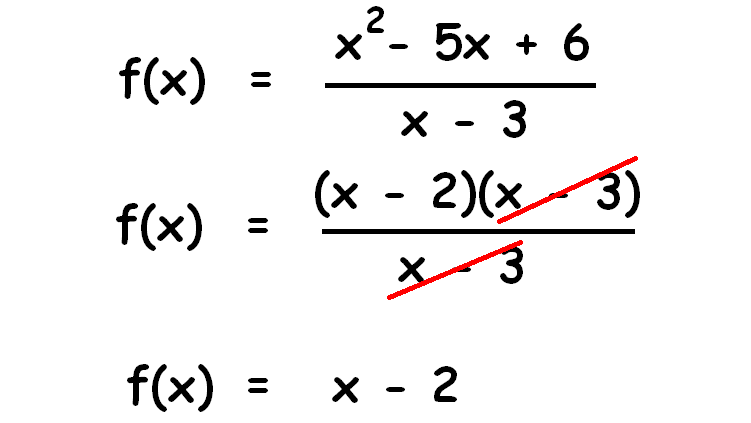
Problem 2 :
Write the equivalent algebraic expression for the expression given below.
4x - (2 + 4x) - ii (x - i) - 8 (ten -three)
Solution:
= 4x - (2 + 4x) - 2 (x - i) - 8 (x -iii)
= 4x - 2 - 4x - 2x + 2 - 8x + 24
= 4x - 4x - 2x - 8x - 2 + 2 + 24
= -10x + 24
Problem 3 :
Write the equivalent algebraic expression for the function defined by
f(x) = (5x + 20) / (7x + 28)
Solution:
Factoring the numerator and denominator of the given rational function, we become
f(x) =5(x + 4) / 7(x + 4)
Getting rid of the common factor (x + 4) at both numerator and denominator, we get
f(x) = 5 / vii
Problem four :
Write the equivalent algebraic expression for the expression given below.
(2x - 7)/5 + (x + 9)/xv - (2x -2)/5
Solution :
= (2 x - 7)/v + (x + 9 )/15 - (two x - 2 )/5
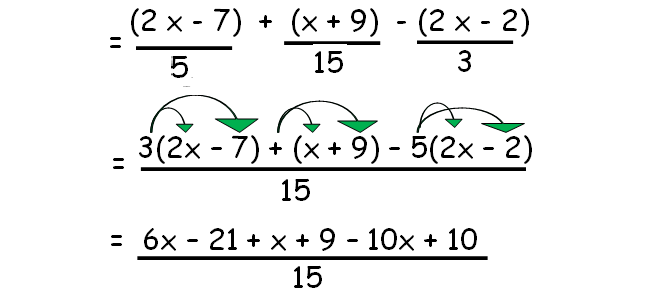
Now we are going to combine the like terms
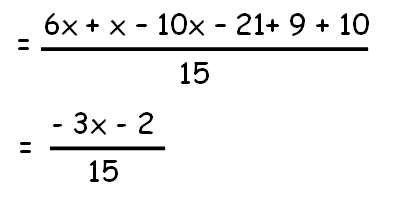
Problem 5 :
Write the equivalent algebraic expression for the expression given below.
(3x + 41) / 2 + (x - 3 ) / 5 - (9 - 2x) / half dozen
Solution :
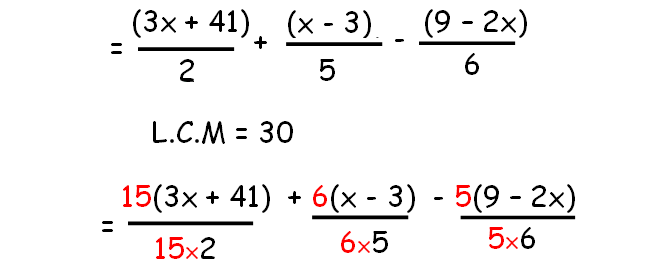
Now we are going to distribute the numbers which is out side the parenthesis to the inner terms.Then combine the like terms

Problem 6 :
Write the equivalent algebraic expression for the function defined by
f(x) = (6x 2 - 54) / (x two + 7x + 12)
Solution:
Factoring the numerator and denominator of the given rational function, we get
f(x) = 6( ten 2 - nine) / (10 + 3)(x + four)
f(x) = half dozen( 10 2 - 3 ii ) / (x + 3)(ten + 4)
f(10) = half-dozen(x + 3)(x - iii) / (x + 3)(x + four)
Getting rid of the common factor (ten + 3) at both numerator and denominator, we get
f(x) = 6(x - 3) / (ten + 4)
Problem 7 :
Write the equivalent algebraic expression for the function defined past
f(x) = (64a 3 + 125b 3 ) / (4a2b + 5ab2 )
Solution:
f(x) = (64 a 3 + 125b iii ) / (4aiib + 5ab2 )
f(x) = (43 a 3 + 5 3 b 3 ) / (4a2b + 5abtwo)
f(x) = [(4 a) iii + (5 b) 3 ] / (4a2b + 5abtwo)
Factoring the numerator and denominator of the given rational office, we get
f(x) = [4a + 5b][(4a)2 - 4a.5b + (5b ) ii ] / ab(4a + 5b)
f(x) = [(4a ) 2 - 4a.5b + (5b ) 2 ] / ab
f(ten) = [16a ii - 20ab + 25b 2 ] / ab
Getting rid of the mutual factor (4a + 5b) at both numerator and denominator, we get
f(x) = [(4a ) 2 - 4a.5b + (5b ) ii ] / ab
f(x) = [16a 2 - 20ab + 25b two ] / ab
Problem 8 :
Write the equivalent algebraic expression for the function defined past
f(10) = (x2 + 7x + ten ) / ( 10 2 - iv )
Solution:
f(x) = ( x 2 + 7x + x ) / ( 10 two - 4 )
f(x) = ( 10 ii + 7x + 10 ) / ( x 2 - ii 2 )
Factoring the numerator and denominator of the given rational function, we go
f(ten) = (ten + 2)(x + 5) / (x + 2)(x - ii)
Getting rid of the common factor (x + 5) at both numerator and denominator, we get
f(x) = (x + 5) / (x - 2)

Apart from stuff given higher up, if you demand whatever other stuff in math, please use our google custom search hither.
Kindly mail your feedback tov4formath@gmail.com
We e'er appreciate your feedback.
© All rights reserved. onlinemath4all.com
rodrigueztherstre.blogspot.com
Source: https://www.onlinemath4all.com/generating-equivalent-algebraic-expressions.html
0 Response to "Generating Equivalent Numerical Expressions Module 9 Page 285 Review"
Post a Comment